How the same evidence can yield different answers when you only change the order.
- The phenomenon: same chunks, different outcomes
- What we can observe during decoding
- A simple instability signal
- Measuring order sensitivity
- What this diagnostic is and is not
- Practical notes
People often treat retrieval order as a formatting detail.
In practice, context order can change the early next token distributions, and that can push decoding into a different trajectory.
This post is about how to measure that sensitivity using only token probabilities.
The phenomenon: same chunks, different outcomes
In many retrieval augmented setups, the model receives a question and a set of retrieved chunks.
If you permute those chunks but keep everything else fixed, you often get different answers.
There are two important points.
First, order effects are not rare edge cases.
They show up even with greedy decoding because the model still makes a sequence of locally optimal choices.
Second, the effect is process level.
You can observe drift before the final answer diverges.
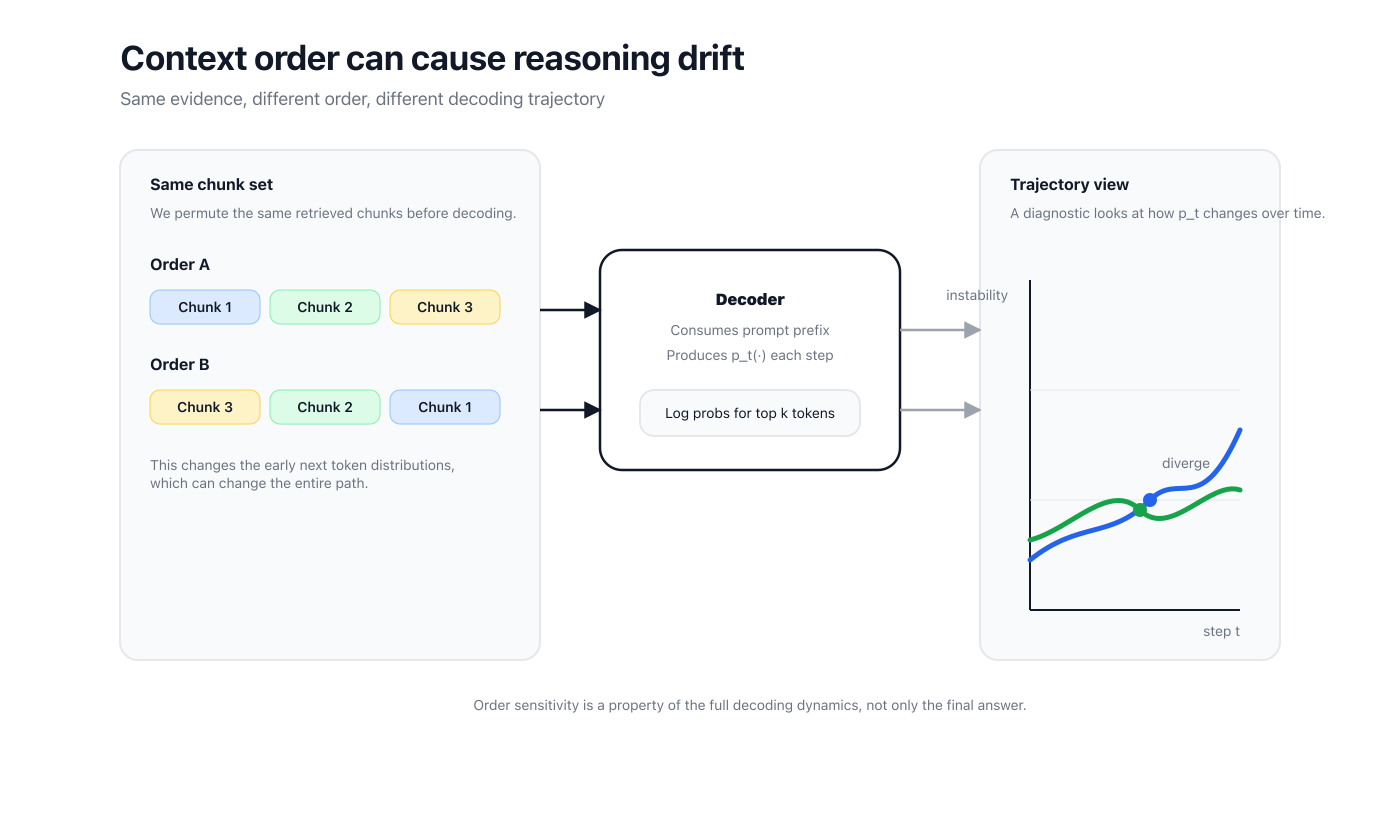
What we can observe during decoding
At each decoding step , an autoregressive model produces a next token distribution .
Many APIs expose only top candidates with log probabilities.
That is enough.
We can renormalize the logged support and compute lightweight signals from the resulting distribution.
The key idea is to measure two things.
- Uncertainty at a step.
- Distributional change from one step to the next.
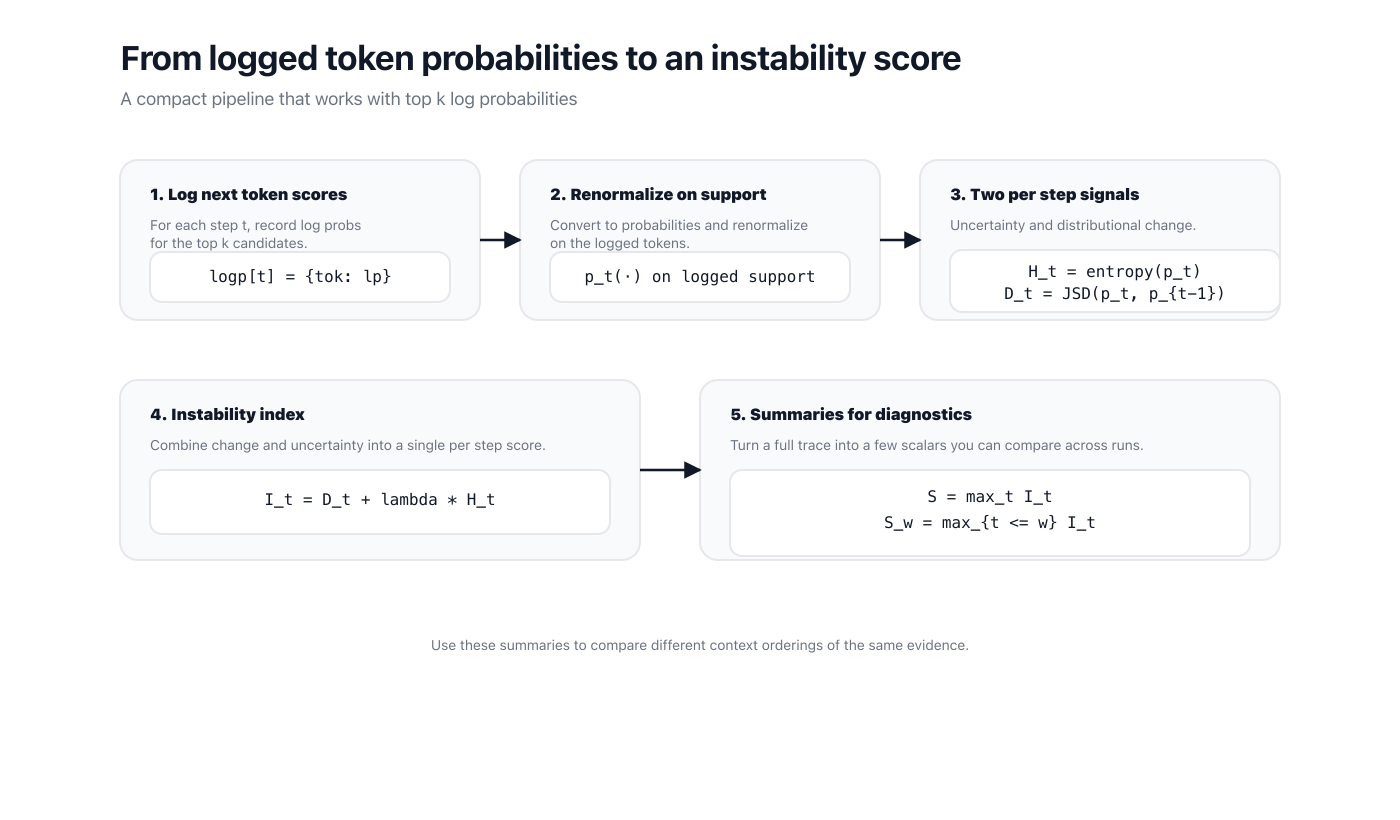
k token probabilities to an instability score and summary statistics.A simple instability signal
Define an entropy term from and a Jensen Shannon divergence term between and .
Then define an instability index
where is a mixing weight.
I use as a default.
To summarize a trace, use a peak statistic.
For early diagnostics, use prefix windows.
This is simple on purpose.
The goal is not a perfect theory of decoding.
The goal is a consistent metric you can compute across many runs.
Measuring order sensitivity
Now we can define a clean protocol.
- Fix a question and its retrieved chunk set.
- Generate multiple permutations of the chunk order.
- Decode with the same settings for each permutation and log top token probabilities.
- Compute , then summarize each run by or .
- Quantify sensitivity from variability across permutations.
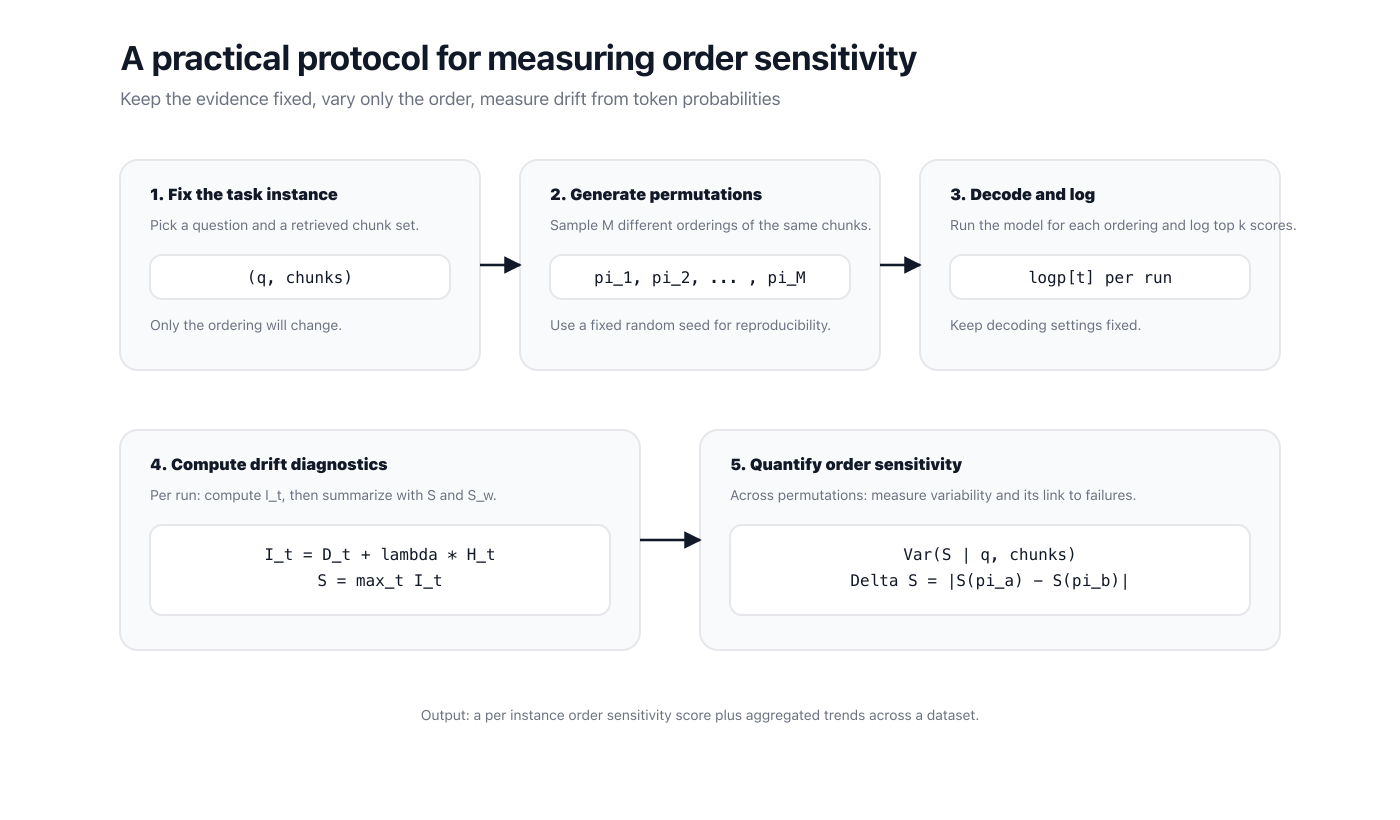
You can report sensitivity in several equivalent ways.
- The fraction of permutations that cross a chosen risk threshold.
If you also label runs as correct or wrong, you can test whether higher sensitivity correlates with a higher chance of failure.
What this diagnostic is and is not
What it is.
- A way to measure how much the decoding path changes under context permutations.
- A method that works with logged token probabilities.
- A tool to compare retrieval and prompting strategies by process dynamics.
What it is not.
- Not an intervention.
- Not a claim that you can eliminate order effects with a single heuristic.
Practical notes
A few details matter in practice.
- Keep decoding settings fixed.
- Keep the chunk set fixed.
- Use a fixed random seed for permutation sampling.
- Use the same stopping rules across runs.
If you have access to full vocabulary logits, compute entropy and divergence on the full distribution.
If you only have top logging, renormalize on the logged support and treat the metric as a consistent approximation.
# Inputs: per step top k logprobs: logp[t] = {token: log_prob}
# Output: instability strength S
def renormalize(logp_dict):
probs = {tok: math.exp(lp) for tok, lp in logp_dict.items()}
z = sum(probs.values())
return {tok: p / z for tok, p in probs.items()}
def entropy(p):
return -sum(pi * math.log(pi) for pi in p.values() if pi > 0.0)
def jsd(p, q):
keys = set(p) | set(q)
m = {k: 0.5 * (p.get(k, 0.0) + q.get(k, 0.0)) for k in keys}
def kl(a, b):
return sum(ai * math.log(ai / b[k]) for k, ai in a.items() if ai > 0.0)
return 0.5 * kl(p, m) + 0.5 * kl(q, m)
p_prev = None
I = []
for t in range(T):
p_t = renormalize(logp[t])
H_t = entropy(p_t)
D_t = 0.0 if p_prev is None else jsd(p_t, p_prev)
I.append(D_t + 1.0 * H_t)
p_prev = p_t
S = max(I)